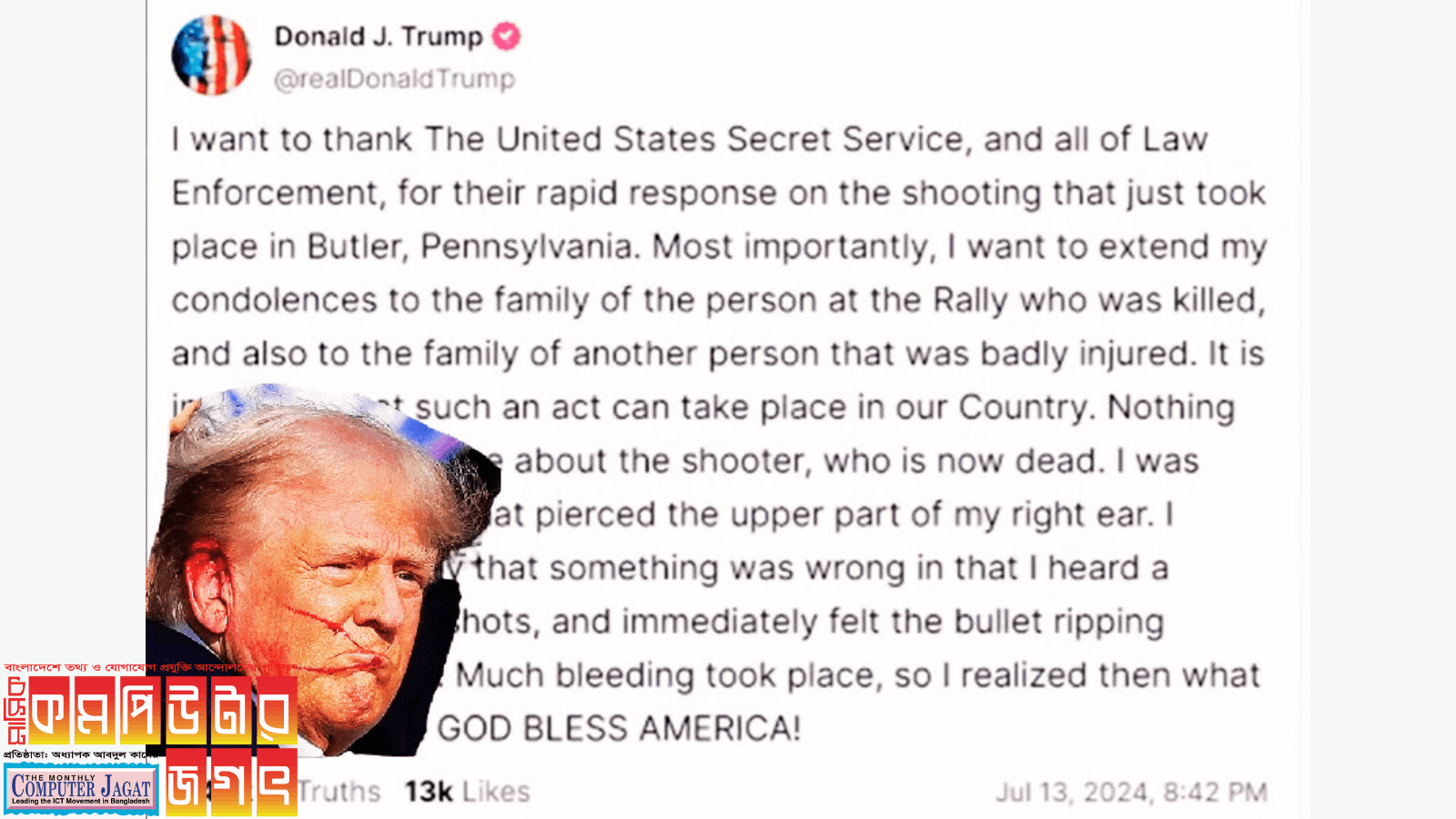
ভাইরাল আইকিউ টেস্ট

১ + ৪ = ০৫

২ + ৫ = ১২

৩ + ৬ = ২১ হলে

৮ + ১১ = ?

কেউ বলছেন, এর উত্তর ৯৬। কারণ, এখানে প্রতিটি লাইনের সমান (=) চিহ্নের বাম পাশের প্রথম সংখাকে ক এবং দ্বিতীয় সংখ্যাকে খ ধরলে এই সংখা দুইটির যোগফল হবে (ক + কী খ)-এর সমান। যেমন-

প্রথম লাইন ১ + ৪ = ০৫ এবং ১ + ১ ক্ম ৪ = ০৫

দ্বিতীয় লাইন ২ + ৫ = ১২ এবং ২ + ২ ক্ম ৫ = ১২

তৃতীয় লাইন ৩ + ৬ = ২১ এবং ৩ + ৩ ক্ম ৬ = ২১

তাহলে চতুর্থ লাইন হওয়া উচিত ৮ + ১১ = ৯৬

কারণ, ৮ + ৮ ক্ম ১১ = ৯৬

অতএব নির্ণেয় উত্তর ৯৬।

কিন্তু অন্যেরা বলছেন, উত্তরটা হবে ৪০। কারণ, আসলে এখানে ধাঁধার প্রতিটি লাইনের যোগফল ধারায় ‘রানিং টোটাল’ বা ‘চলমান সমষ্টিফল’কে পরবর্তী লাইনে যোগ করা হয়েছে। যেমন-

প্রথম লাইন : ১ + ৪ = ০৫

দ্বিতীয় লাইন : ৫ + ২ + ৫ = ১২

তৃতীয় লাইন : ১২ + ৩ + ৬ = ২১

অতএব চতুর্থ লাইন হবে : ২১ + ৮ + ১১ = ৪০

অতএব সঠিক উত্তরটি হচ্ছে ৪০। অর্থাৎ এখানে ধাঁধাটির শেষ লাইনে ৮ + ১১ = ৪০ হবে।

তাহলে আমরা যদি প্রদত্ত প্রশ্নের উত্তর খুঁজতে যাই, তবে এর দুইটি উত্তর পাই। যদি ‘ক ও খ-এর যোগফল = ক + ক ক্ম খ’ প্যাটার্নটি অনুসরণ করি, তবে উত্তরটা আসে ৯৬। আর ‘রানিং টোটাল’ প্যাটার্ন অনুসরণ করলে আমরা উত্তরটা পাই ৪০।

আবার ‘রানিং টোটাল’ বা ‘চলমান সমষ্টিফল’ প্যাটার্ন নিয়ে একটু ভিন্নভাবে চিন্তা করতে পারি। প্রশ্নটির পথম তিন লাইন এরূপ-

১ + ৪ = ০৫, ২ + ৫ = ১২ এবং ৩ + ৬ = ২১

অর্থাৎ সমান (=) চিহ্নের বামের যোগচিহ্নের বামের সংখ্যার মতো ডানের সংখ্যাও এক-এক করে বাড়িয়ে পরবর্তী লাইনগুলো লেখা হয়েছে। কিন্তু চতুর্থ লাইনে এসে যোগচিহ্নের ডানের ও বামের সংখ্যা উভয়ের ক্ষক্ষত্রে এক লাফে ৫ বাড়িয়ে লেখা হয়েছে ৮ + ১১ = ?। অর্থাৎ, এখানে তৃতীয় লাইনের পর চারটি লাইন বাদ পড়ে গেছে। এই বাদ পড়া লাইন বা মিসিং লাইনগুলো লেখা হলে ধারাটি হতো এমন-

১ + ৪ = ০৫, ২ + ৫ = ১২, ৩ + ৬ = ২১, ৪ + ৭ = ৩২, ৫ + ৮ = ৪৫, ৬ + ৯ = ৬০, ৭ + ১০ =৭৭, ৮ + ১১ = ?

এখন এসব লাইনে ‘রানিং টোটাল’ প্যাটার্ন প্রয়োগ করলে সমাধানটি দাঁড়াবে এমন-

১ + ৪ = ০৫, ০৫ + ২ + ৫ = ১২, ১২ + ৩ + ৬ = ২১, ২১ + ৪ + ৭ = ৩২, ৩২ + ৫ + ৮ = ৪৫, ৪৫ + ৬ + ৯ = ৬০, ৬০ + ৭ + ১০ = ৭৭, ৭৭ + ৮ + ১১ = ৯৬

অতএব এখানে প্রদত্ত ৮ + ১১ = ? প্রশ্নের উত্তরটা আমরা পাচ্ছি ৯৬।

সুতরাং প্রথম প্যাটার্ন বিবেচনা করে আমরা প্রদত্ত প্রশ্নের উত্তর পেয়েছি ৯৬। দ্বিতীয় প্যাটার্ন বিবেচনায় এর উত্তর পেয়েছি ৪০। আর সবশেষ প্যাটার্ন অনুসরণ করে প্রশ্নের উত্তর আবারও পেলাম ৯৬।

তাহলে প্রশ্ন আসে কোন উত্তরটি সঠিক ৯৬ না ৪০? এর জবাবে বলা যায়, যিনি যে উত্তর দেবেন তার অনুসৃত প্যাটার্নটি যদি যথাযথভাবে যৌক্তিক হয়, তবে তার উত্তরটি গ্রহণযোগ্য বিবেচ্য হবে। এ ধরনের ভাইরাল টেস্টে একাধিক উত্তর থাকতেই পারে। যেমনটি আমাদের এই প্রশ্নটির ক্ষক্ষত্রে আমরা দুইটি সঠিক উত্তর পেয়েছি ৯৬ ও ৪০। আবার অন্য কেউ ভিন্ন কোনো প্যাটার্ন অনুসরণ করে তৃতীয় কোনো সমাধান বের করতে পারলে তাও গ্রহণযোগ্য হতে পারে।

সব সময় শেষফল ১০৮৯

তিন অঙ্কের যেকোনো একটি সংখ্যা নিই। ধরি, সেটি ৭৪১। এবার সংখ্যাটি উল্টো করে লিখলে পাব ১৪৭। এই সংখ্যা দুইটির মধ্যে বড়টি থেকে ছোটটি বিয়োগ করি। তাহলে বিয়োগফল পাই ৭৪১ - ১৪৭ = ৫৯৪। এই ৫৯৪ উল্টো করে লিখলে হয় ৪৯৫। এখন ৫৯৪ ও ৪৯৫ যোগ করলে যোগফল হয় ১০৮৯। তাহলে এখানে শেষফল পাওয়া গেল ১০৮৯।

এবার তিন অঙ্কের আরেকটি সংখ্যা নিই। ধরি, এবারের সংখ্যাটি ৩৪২। এটি উল্টো করে লিখলে হয় ২৪৩। এখানে ৩৪২ বড়, ২৪৩ ছোট। বড়টি থেকে ছোটটি বিয়োগ করলে পাই ৩৪২ - ২৪৩ = ০৯৯। বিশেষভাবে মনে রাখতে হবে, এই বিয়োগফলকে তিন অঙ্কের আকারে লিখতে হবে। তাই বিয়োগফলটি ৯৯ না লিখে ০৯৯ আকারে লেখা হয়েছে। এখন ০৯৯-কে উল্টো করে লিখলে হয় ৯৯০। আর এই ০৯৯ ও ৯৯০-এর যোগফল আগের মতোই হয় ১০৮৯।

ওপরের দুইটি উদাহরণেই ধারাবাহিকভাবে একই ধরনের গাণিতিক পদ্ধতি অনুসরণ করা হয়েছে এবং উভয় ক্ষক্ষত্রেই শেষফলটি পাওয়া গেছে ১০৮৯। এভাবে আমরা তিন অঙ্কের যেকোনো একটি সংখ্যা নিয়ে ওপরের উদাহরণ দুইটির মতো ধারাবাহিকভাবে গাণিতিক পদ্ধতিগুলো প্রয়োগ করি, তবে সম সময় শেষফলটি পাব ১০৮৯।

রহস্যটা কোথায় : এবার আমরা জানার চেষ্টা করব কেনো এমন হয়, সব সময়ই শেষফলটা ১০৮৯ হয়, এর রহসটা কোথায়? আমরা শুরুটা করেছি একটি তিন অঙ্কের সংখ্যা নিয়ে। এই সংখ্যাটির শতকের ঘরে একটি অঙ্ক, দশকের ঘরে একটি অঙ্ক এবং এককের ঘরে একটি অঙ্ক থাকবে। ধরি, এই অঙ্ক তিনটি যথাক্রমে ক, খ ও গ। আর সংখ্যাটি তখন হবে এমন- কখগ। আর এর উল্টো সংখ্যাটি হবে গখক। এই সংখ্যা দুইটির বিয়োগ ফল দাঁড়াবে-

কখগ - গখক = (১০০ক + ১০খ + ১গ) - (১০০গ + ১০খ + ১ক)

= (১০০ক - ১ক) + (১০খ - ১০খ) + (১গ - ১০০গ)

= ৯৯ক - ৯৯গ

= ৯৯ (ক - গ)

আমরা জানি ক ও গ হচ্ছে ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯ বা ০-এর যেকোনো একটি অঙ্ক। অতএব (ক - গ)-এর মানও হতে পারে ১ থেকে ৯-এর মধ্যকার যেকোনো একটি অঙ্ক। তাহলে ওপরে পাওয়া (কখগ - গখক)-এর মান, অর্থাৎ ৯৯ (ক - গ)-এর মান হতে পারে নিচের যেকোনো একটি-

৯৯ ক্ম ১ = ০৯৯, ৯৯ ক্ম ২ = ১৯৮, ৯৯ ক্ম ৩ = ২৯৭, ৯৯ ক্ম ৪ = ৩৯৬, ৯৯ ক্ম ৫ = ৪৯৫, ৯৯ ক্ম ৬ = ৫৯৪, ৯৯ ক্ম ৭ = ৬৯৩, ৯৯ ক্ম ৮ = ৭৯২, ৯৯ ক্ম ৯ = ৮৯১

এই সংখ্যাগুলোকে যদি আমরা কখগ বা গখক, তবে আকারে ভাবি, মাঝখানের খ-এর মান প্রত্যেকটি সংখ্যায় ৯ হবে। অর্থাৎ খ = ৯। আবার লক্ষ করি, প্রতিটি সংখ্যায় প্রথম ও শেষ অঙ্কের যোগফল ৯, অর্থাৎ ক + গ = ৯।

ওপরের দুটি উদাহরণেই আমরা প্রথমে প্রদত্ত সংখ্যা ও এটি উল্টো করে লিখে এ দুটির বিয়োগফল অর্থাৎ (কখগ - গখক)-এর মান বের করেছিলাম। শেষাংশে বিয়োগফল ও এর উল্টো সংখ্যার যোগফল, অর্থাৎ (কখগ + গখক)-এর মান বের করে দেখেছিলাম এই মান সব সময় হয় ১০৮৯। এখানে-

কখগ + গখক = (১০০ক + ১০ খ + ১গ) + (১০০গ + ১০খ + ১ক)

= ১০১ক +১০১গ + ২০খ

= ১০১ (ক + গ) + ২০ খ

= ১০১ ক্ম ৯ + ২০ ক্ম ৯

= ৯০৯ + ১৮০

= ১০৮৯

অতএব এ ক্ষক্ষত্রেও শেষফল আসে ১০৮৯। তাই যেকোনো তিন অঙ্কের সংখ্যার ক্ষক্ষত্রে ওপরের কৌশলটি প্রযোজ্য হবে।

গণিতদাদু